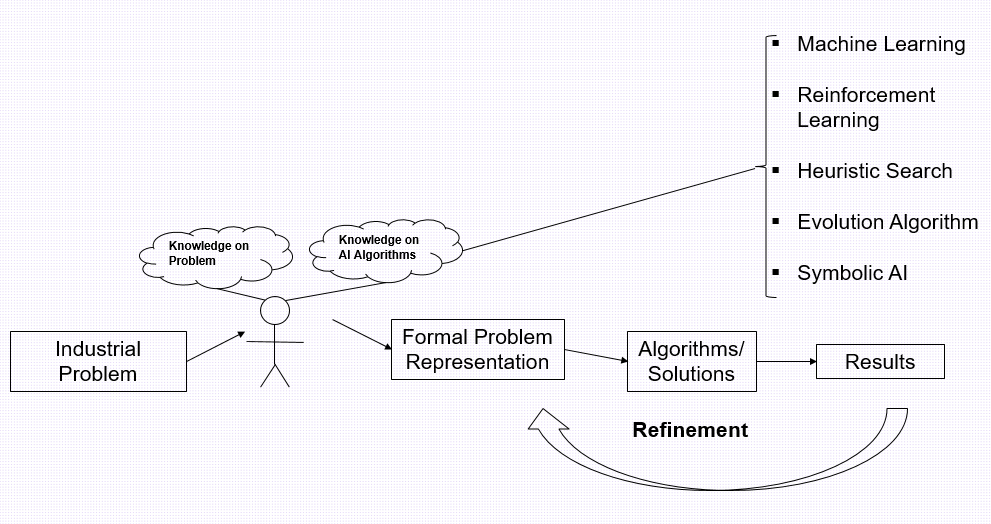
Compilers are inherently designed to abridge the gap between software and hardware. In the same sense, machine learning compilers are primarily developed for hardware for machine learning programs, e.g., deep neural networks.
AI accelerators
Due to the successes of deep neural networks and other machine learning applications, specific hardware devicies have been developed for these computer programs. These hardware might be collectively referred to as AI accelerators, as their major aim is to accelerate tensor program computations.
In below I list some chips that might be used for AI computation:
- CPUs – this is the most generic chips we see everday, and of course, they are able to execute tensor programs though it has high latency.
- NVIDIA GPUs, e.g., microarchitectures Volta, 2017, Turing, 2018, and Ampere, 2020
- Google’s TPUs. So far, four versions have been released, i.e., TPU-v1 in 2016, TPU-v2 in 2017, TPU-v3 in 2018, and TPU-v4 in 2021. An Edge TPU is announced in 2018, and has been used in Pixel-4 smart phone.
- Huawei’s Ascend Series.
See paper (Ascend: a Scalable and Unified Architecture for Ubiquitous Deep Neural Network Computing : Industry Track Paper)
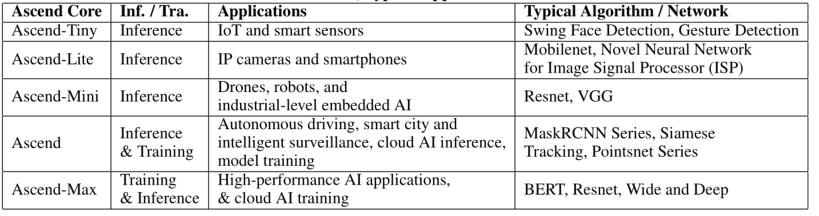
- Others: they are many other AI accelerators.
Tensor programs software frameworks (neural net frameworks)
Having only a dedicated hardware is insufficient to accelerating tensor program computations. They need also software support. Over the past few years, many neural network frameworks have been developed. To name a few, Tensorflow, Pytorch, JAX, and Huawei’s Mindspore.
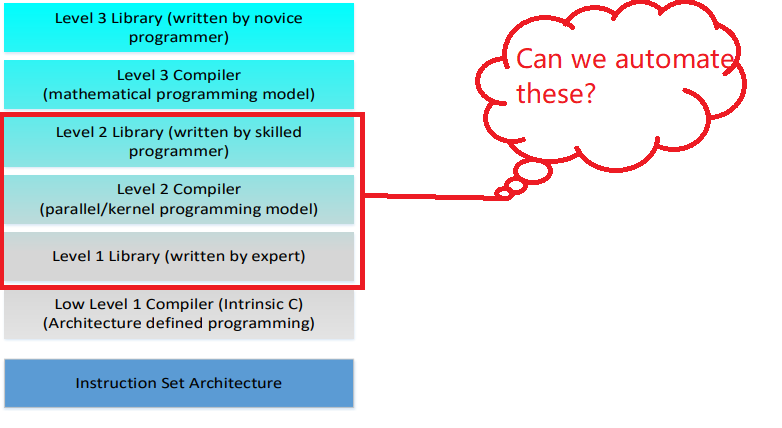
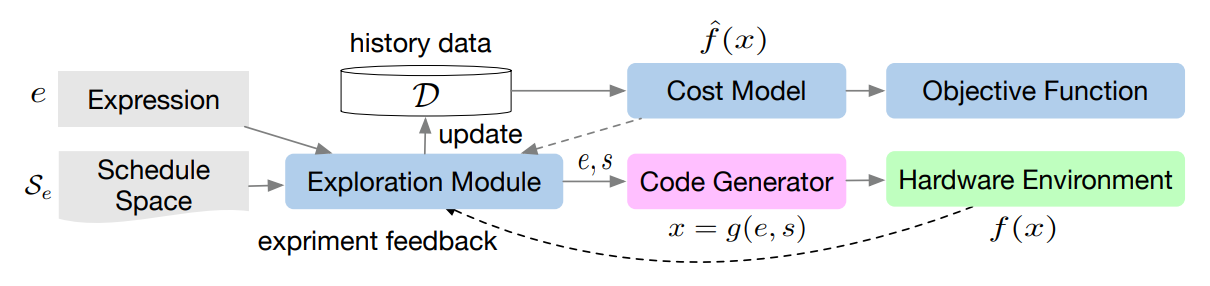
These frameworks are all created under the above software architecture stack, among which the core question being addressed is how to translate high-level and hardware-agnostic code into low-level, efficient and hardware-aware code. In fact, this core task is fairly identical despite how different these software frameworks may look in appearance. Thus, deep learning compilers do have the right of being exist as standalone projects. Some of them are listed in below.
Machine compilers
This specifically refers to the “intermidiate” part of the software framework above.
-
XLA
XLA, developed by Google, originally for tensorflow, but now also supports Pytorch, JAX.
-
GLOW
GLOW, developed by Facebook.
-
Tiramisu
Tiramisu, developed by MIT.
-
TensorComprehensions
TensorComprehensions by Facebook.
-
AutoTVM
AutoTVM, as the name indicates, is developed in TVM, but it supports also many other front-ends, e.g. Tensorflow, Pytorch etc.
-
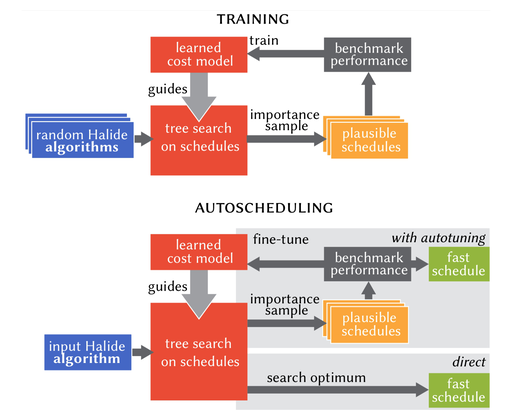
Halide
Halide is a language in
C++as well as a compiler. It was first created for accelerating image processing pipelines, but can also be used for deep neural network models, given that the model specification has been converted into Halide’sC++language.
Difference Summary
In summary, the differences of these tools are majorly reflected in the following aspects:
-
frontend language expressiveness. For example, Halide does not support cyclic computation graphs, e.g., LSTMs.
-
search space modelling. For example, Tiramisu models the scheduling space using
Polyhedral, while Halide models the search space as a decision tree. -
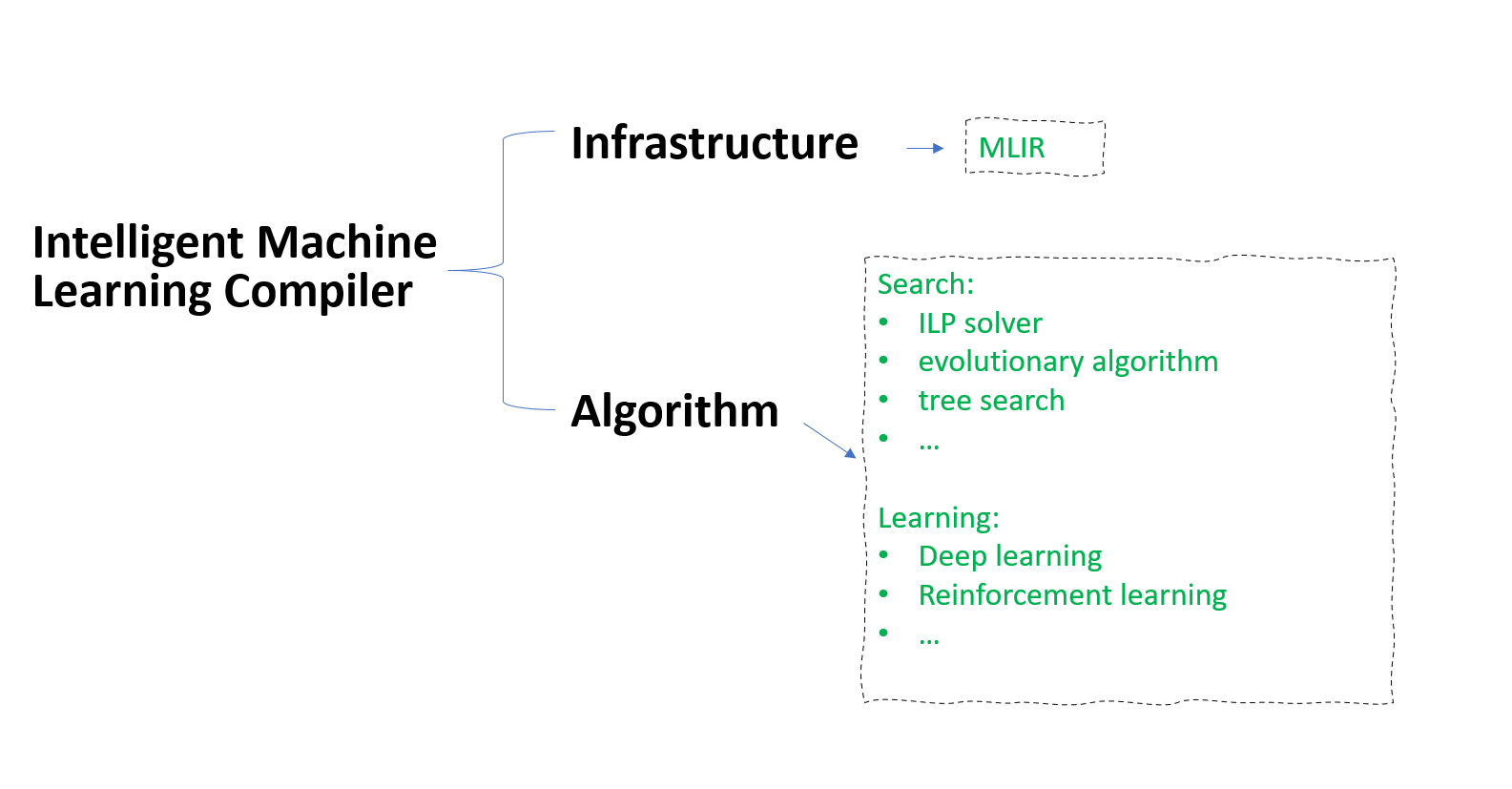
algorithms for scheduling. For example, Tiramisu uses ILP solver. AutoTVM used evolutionary algorithms. Halide uses tree search.
-
backend support
MLIR
Besides the algorithmic differences, all the tools above rely certain format of intermidate representation, which is usually developed for that specific tool. It would ideal that design on this aspect can be standardized, thus different compilers can mostly focus on developing intelligent compilation algorithms, rather than engineering seemingly different but in-theory equivalent designs. The MLIR represnets an effort towards unifying these intermediate representations.