The idea of reinforcement learning has been applied for scheduling tensor programs, but so far, the RL algorithms being used are largely different from those being developed in the RL community. In this blog, I briefly summarize the existing methods, and dicuss potential and interesting working directions.

Halide

The 2019 Halide auto-scheduler combines heuristic search and neural net for scheduling tensor programs (even though neural nets are tensor programs themselves). The Adams2019 auto-scheduler’s algorithm can be summarized in the following diagram.

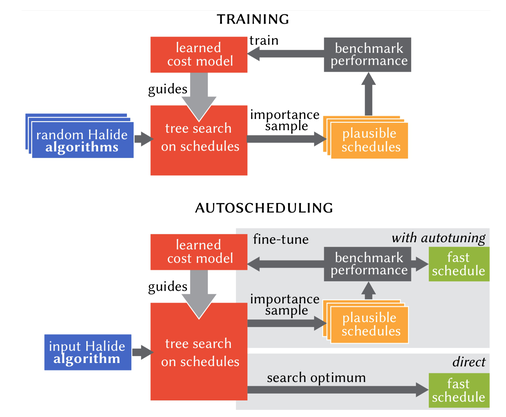
AutotVM

The TVM auto-scheduler shares a similar spirit with Halide, see below:

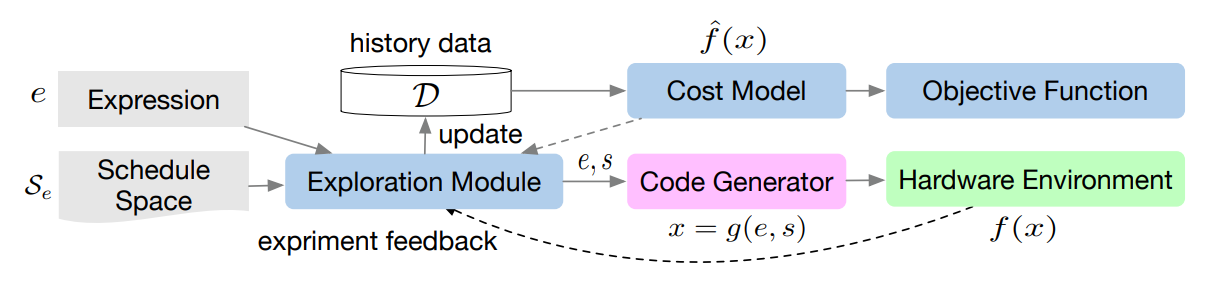
Althought the algorithmic details in these auto-schedulers are quite different. They do share the same high-level structure:

• They all conduct a search with a pretrained neural net model — Halide uses tree search, while AutoTVM used simulated annealing.
• They all contain a sampling and benchmarking procedure for collecting schedule dataset.
• They all contain a procedure for training the neural net used in search.

These three aspects are exactly in line with the search-based RL framework in AlphaGo or AlphaZero. Naturally, if any further development is conducted on one of these three directions, a better auto-schedulers is expected to produce. Indeed, this is also what is happening in reality.

• Updated Halide auto-scheduler for GPU designed a new and improved tree-search algorithm. See Efficient automatic scheduling of imaging and vision pipelines for the GPU
• Updated AutoTVM, namely Ansor used more advanced genetic algorithm for searching. See Ansor : Generating High-Performance Tensor Programs for Deep Learning

Yet, one more important solution step we overlooked above is how the search space of schedules are defined. Clearly, these search spaces cannot be directly extracted from our sketchy description of the problem using natural language — there must be a formal definition by which the space of schedules can be generated and searched systematically (like in games, we need action definition and rules to control action transitions). Indeed, in both Halide and TVM, the definition of search space is also an important (possibly not less important than the algorithms for searching & learning) task that requires yet another kind of algorithm for automatic modelling.

In my view, the search space modelling algorithm would have to come a trade-off between the following properties:

• Easy to encode — thus engineers can write easy-to-understand and maintainable code.
• Compact — this refers a balance of the following to qualities:
  • Adequate coverage: it should cover enough high-quality schedules.
  • Minimum redundancy: it should not include too many meaningless schedules.
• Structural convenient — this refers to a well-formed structure that might be harnessed by the searching algorithm. For example, the Polyhedral method tries to formulate the schedule space using a set of integer linear equations, thus many well-developed ILP solver can be directly applied for searching the optimal schedule.

Once search space modelling is settled, i.e., problem is formally defined, algorithms development can focus on heuristic search, machine learning and the combination of both. The overall algorithm framework is thus a search-based reinforcement learning.